Can’t hear? Turn up the white noise, says a team of Rutgers-Camden
professors who have produced a mathematical explanation for the
benefits of noise. Their findings could lead to major improvements in
hearing aid technology.
Dawei Hong, a computer scientist, and biologists Joseph Martin and
William Saidel are using mathematics to explain the biological benefits
of noise.
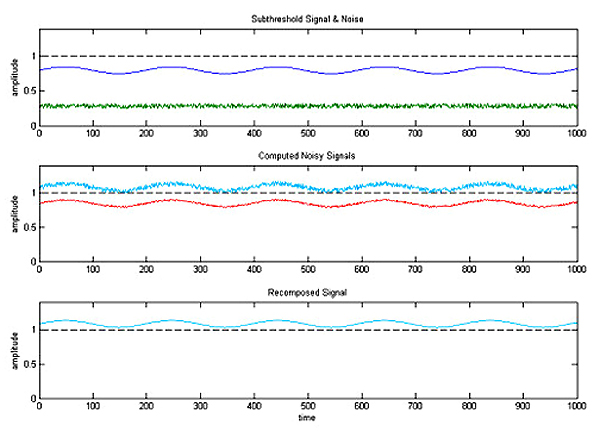
The Rutgers-Camden team’s breakthrough mathematical theory is
comprehensive, explaining or accounting for all observed situations
where noise actually increases the ability to hear. To develop the
theory – actually a mathematical expression like E=mc2 – Hong and his
colleagues employed a variation on the wavelet technique, a standard
method used in cleaning up digital images. The scientists’ discovery
could have numerous applications – most obviously in treating hearing
loss by artificially increasing the amount of noise in the cochlea of
the inner ear, perhaps by an implanted device.
Although the Camden research team studied noise in the auditory
system, for example, “white noise” or “noise-in-the channel,” noise
also can refer to other random phenomena in biological systems and the
natural world where it may be a fundamental feature.
The team applied this principle of noise to a process called “quorum
sensing” in bacteria. How bacteria signal one another to coordinate
certain behavior and act collectively – such as when causing an
infection – may be based on “noise” in the cellular environment.
The researchers used bacteria as a starting point for observing how
noise affects cell-to-cell communication. A full understanding of how
this simple form of communication works might show how to disrupt it,
and the resulting infection. The team will next apply their idea to the
nervous system, where the cell’s entire job is to communicate.